Comment Calculer Le Volume D Un Tétraèdre

Étant donné la longueur des arêtes d'un tétraèdre irrégulier. La tâche est de déterminer le volume de ce tétraèdre.
Soit la longueur des arêtes des pyramides soit u, U, 5, 5, w, W.

La formule pour calculer le volume d'un tétraèdre irrégulier en fonction de ses longueurs d'arête est :
A =

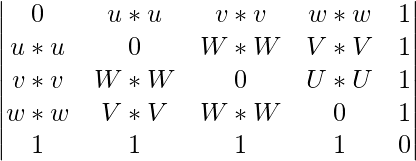
C++

// C++ implementation of higher up approach #include <$.25/stdc++.h> using namespace std; #define db double // Function to observe the volume void findVolume(db u, db v, db westward, db U, db V, db W, db b) {       // Steps to calculate volume of a     // Tetrahedron using formula     db uPow = prisoner of war(u, two);     db vPow = pow(v, ii);     db wPow = pow(westward, 2);     db UPow = pw(U, 2);     db VPow = pow(V, 2);     db WPow = pow(W, 2);       db a = 4 * (uPow * vPow * wPow)         - uPow * pow((vPow + wPow - UPow), 2)         - vPow * pw((wPow + uPow - VPow), ii)         - wPow * pow((uPow + vPow - WPow), two)         + (vPow + wPow - UPow) * (wPow + uPow - VPow)         * (uPow + vPow - WPow);     db vol = sqrt(a);     vol /= b;       cout << stock-still << setprecision(4) << vol; }   // Commuter code int main() {       // edge lengths     db u = 1000, five = g, w = 1000;     db U = 3, V = 4, W = 5;     db b = 12;       findVolume(u, five, w, U, V, W, b);       return 0; }          

Java

// Java implementation of above approach   import coffee.util.*; import java.lang.*; import coffee.io.*;     class GFG{   // Function to find the book static void findVolume(double u, double five, double w, double U,                       double 5, double Due west, double b) {       // Steps to calculate volume of a     // Tetrahedron using formula     double uPow = Math.pow(u, 2);     double vPow = Math.pow(5, two);     double wPow = Math.pow(w, 2);     double UPow = Math.pow(U, 2);     double VPow = Math.pow(5, 2);     double WPow = Math.pow(Due west, 2);       double a = 4 * (uPow * vPow * wPow)         - uPow * Math.pow((vPow + wPow - UPow), 2)         - vPow * Math.pow((wPow + uPow - VPow), two)         - wPow * Math.pow((uPow + vPow - WPow), 2)         + (vPow + wPow - UPow) * (wPow + uPow - VPow)         * (uPow + vPow - WPow);     double vol = Math.sqrt(a);     vol /= b;       System.out.printf("%.4f",vol); }   // Driver code public static void master(String args[]) {       // edge lengths     double u = one thousand, v = yard, w = 1000;     double U = iii, V = 4, Westward = v;     double b = 12;       findVolume(u, v, w, U, V, Westward, b); }       }          

Python3

# Python 3 implementation of above approach   # from math lib import everything from math import *   # Function to observe the book def findVolume(u, five, west, U, V, W, b) :         # Steps to calculate volume of a     # Tetrahedron using formula     uPow = pw(u, 2)     vPow = prisoner of war(v, 2)     wPow = pow(w, 2)     UPow = pw(U, 2)     VPow = pow(V, 2)     WPow = pow(W, 2)         a = (iv * (uPow * vPow * wPow)         - uPow * pw((vPow + wPow - UPow), 2)         - vPow * prisoner of war((wPow + uPow - VPow), two)         - wPow * pow((uPow + vPow - WPow), 2)         + (vPow + wPow - UPow) * (wPow + uPow - VPow)         * (uPow + vPow - WPow))               vol = sqrt(a)     vol /= b         impress(round(vol,iv))    # Driver lawmaking     if __name__ == "__main__" :       # border lengths     u, five, w = 1000, 1000, grand     U, V, W = 3, 4, 5     b = 12         findVolume(u, v, w, U, V, W, b)     # This code is contributed by ANKITRAI1          

C#

// C# implementation of to a higher place approach using System;   class GFG {   // Function to find the volume static void findVolume(double u, double v,                        double w, double U,                        double V, double W,                        double b) {       // Steps to calculate volume of a     // Tetrahedron using formula     double uPow = Math.Pw(u, 2);     double vPow = Math.Pow(five, 2);     double wPow = Math.Prisoner of war(west, 2);     double UPow = Math.Prisoner of war(U, ii);     double VPow = Math.Pow(Five, two);     double WPow = Math.Pow(Due west, 2);       double a = four * (uPow * vPow * wPow) -                     uPow * Math.Pow((vPow + wPow - UPow), ii) -                     vPow * Math.Pw((wPow + uPow - VPow), 2) -                     wPow * Math.Prisoner of war((uPow + vPow - WPow), 2) +                     (vPow + wPow - UPow) *                     (wPow + uPow - VPow) * (uPow + vPow - WPow);     double vol = Math.Sqrt(a);     vol /= b;       Console.Write(Organization.Math.Round(vol, 4)); }   // Driver code public static void Principal() {       // edge lengths     double u = one thousand, v = 1000, westward = m;     double U = three, V = four, W = 5;     double b = 12;       findVolume(u, 5, w, U, V, W, b); } }   // This code is contributed // by ChitraNayal          

PHP

<?php // PHP implementation of above approach   // Office to find the book role findVolume($u, $five, $w,                     $U, $V, $Due west, $b) {       // Steps to calculate book of     // a Tetrahedron using formula     $uPow = pow($u, 2);     $vPow = pow($5, 2);     $wPow = pow($w, 2);     $UPow = pow($U, two);     $VPow = pow($V, two);     $WPow = pow($Westward, two);       $a = 4 * ($uPow * $vPow * $wPow) -               $uPow * pow(($vPow + $wPow - $UPow), 2) -               $vPow * prisoner of war(($wPow + $uPow - $VPow), 2) -               $wPow * pow(($uPow + $vPow - $WPow), two) +               ($vPow + $wPow - $UPow) *               ($wPow + $uPow - $VPow) *               ($uPow + $vPow - $WPow);     $vol = sqrt($a);     $vol /= $b;       echo $vol; }   // Driver lawmaking   // edge lengths $u = 1000; $v = 1000; $due west = 1000; $U = 3; $V = four; $W = v; $b = 12;   findVolume($u, $v, $w, $U, $Five, $W, $b);   // This lawmaking is contributed // by Shivi_Aggarwal ?>          

Javascript

<script>   // Javascript implementation of higher up approach       // Office to find the volume function findVolume(u, 5, westward, U, V, Due west, b) {           // Steps to calculate book of a     // Tetrahedron using formula     let uPow = Math.prisoner of war(u, 2);     let vPow = Math.pw(five, ii);     let wPow = Math.pow(w, 2);     let UPow = Math.pow(U, 2);     let VPow = Math.prisoner of war(V, 2);     let WPow = Math.prisoner of war(Westward, 2);           let a = four * (uPow * vPow * wPow) -           uPow * Math.pow((vPow + wPow - UPow), two) -           vPow * Math.pow((wPow + uPow - VPow), 2) -           wPow * Math.prisoner of war((uPow + vPow - WPow), 2) +           (vPow + wPow - UPow) * (wPow + uPow - VPow) *           (uPow + vPow - WPow);                 let vol = Math.sqrt(a);     vol /= b;           certificate.write(vol.toFixed(4)); }   // Driver code   // Border lengths let u = yard, v = 1000, west = 1000; let U = three, V = 4, W = five; allow b = 12;   findVolume(u, v, w, U, 5, W, b);   // This code is contributed past avanitrachhadiya2155   </script>          

Comment Calculer Le Volume D Un Tétraèdre,

Source: https://fr.acervolima.com/programme-pour-trouver-le-volume-d-un-tetraedre-irregulier/

Posted by: pontonthereaming.blogspot.com

Share this post